
どうも, みなさんこんにちは。
高橋佳佑です。
今回は入試でもよく見かける「不等式の成立条件」についてお話しします。
単純な不等式は解けるけど, 応用問題になるとどうしていいか分からないという人も多いのではないでしょうか。
数学Ⅰ, Ⅱ, Ⅲそれぞれでいろいろなグラフを学習すると思いますが, グラフを利用して不等式を考えてみましょう。
目次
不等式とグラフの関係
まずは下の例題を考えてみましょう。
下のグラフはある日の東京と沖縄の気温変化をまとめたものである。この日, 東京の気温が沖縄の気温より高いのはおよそ何時か。
![]()
今回問われているのは「東京の気温\(>\)沖縄の気温」となる時間です。グラフからおよそ10時から17時の間であることは分かると思います。具体的な気温を調べなくてもグラフの位置関係から読み取ることができます。
不等式は数の大小関係であり, グラフの上下関係であるということです。
グラフの概形, 方程式や不等式, 最大値と最小値を意識して学習する
高校数学ではいろいろな関数を学習します。その都度, グラフの概形, 方程式や不等式, 最大値と最小値に関して, しっかりと意識して学習しましょう。
数学Ⅰ「二次不等式の成立条件」
より実践的な問題を考えてみましょう。
すべての実数\(x\)に対して不等式\(x^2+2ax+1>0\)が成り立つような定数\(a\)の値の範囲を求めよ。
二次不等式の成立条件に関する問題です。この問題の有名な解法は判別式によるものですが, 判別式による解法は使える状況が限られているというデメリットがあります。なのでここでは応用の利く解法を考えてみましょう。
不等式は数の大小,グラフの上下関係
不等式は数の大小であり, グラフの上下関係です。
この状態は, 「\(x^2+2ax+1\)の最小値が正」と言い換えることができます。
\(x^2+2ax+1=(x+a)^2-a^2+1\)ですから,\(x^2+2ax+1\)の最小値は\(-a^2+1\)です。
よって, 求める\(a\)の範囲は
\begin{align*}
-a^2+1&>0\\
1&>a^2\\
-1&<a<1\\
\end{align*}
となります。
この解法のメリットは, グラフが書ければ二次であろうが三次であろうが解答可能であるということです。以下ではいろいろな不等式の成立条件を考えてみます。
数学Ⅱ「三次不等式の成立条件」
二次不等式の成立条件と同様にグラフを利用して最大値や最小値に注目して三次不等式の成立条件を考えてみましょう。
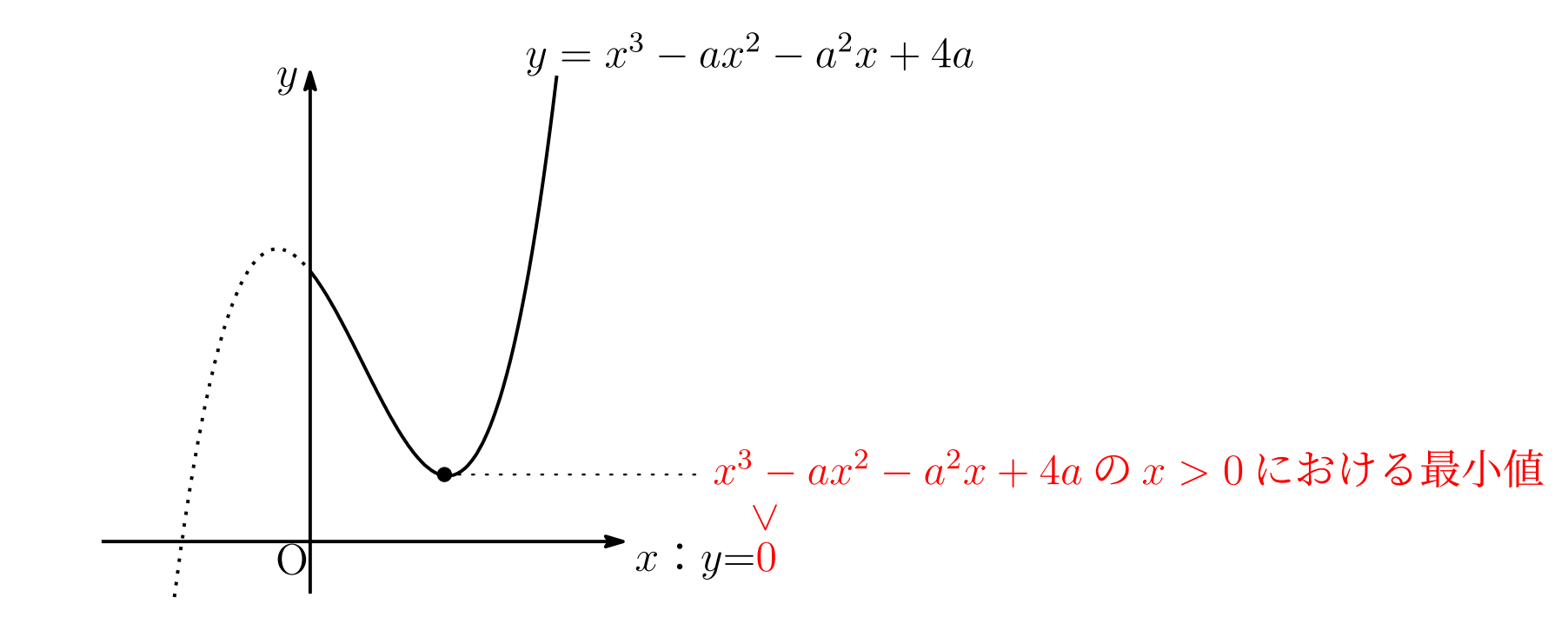
\(a\)を正の定数とする。すべての\(x\)>0に対して不等式\(x^3-ax^2-a^2x+4a>0\)が成り立つような定数\(a\)の値の範囲を求めよ。
解答の方針を整理する
三次関数のグラフの書き方は, 数学Ⅱで学習します。解答の方針を整理しましょう。
\(f(x)=x^3-ax^2-a^2x+4a\)とおいて, \(x>0\)の範囲の増減を調べてみます。
\(a>0\)で\(f'(x)=3x^2-2ax-a^2=(3x+a)(x-a)\)であるから, 増減表は下のようになります。
![]()
\(f(x)\)は\(x>0\)の範囲で最小値\(f(a)=-a^3+4a\)と取るから,
$$-a^3+4a>0$$
\(a>0\)なので両辺\(-a\)で割ると\(a^2-4<0\)となり不等式の解は\(-2<a<2\)となります。いま, \(a>0\)なので求める範囲は\(0<a<2\)となります。
数学Ⅲ「不等式の成立条件」
![]()
数学Ⅲに入るといろいろな関数が微分できるようになるため, 書けるグラフの種類が増え, 最大値や最小値を求められるようになります。つまり, いろいろな不等式の成立条件を考えることが可能になります。
すべての\(x\)>0に対して不等式\(ax\geqq\log x\)が成り立つような定数\(a\)の値の範囲を求めよ。ただし, \(\log x\)は自然対数とする。
不等式の変形
まずは不等式を変形します。文字定数\(a\)を分離することでグラフを書きやすくしましょう。
$$a\geqq\frac{\log x}{x}$$
解答の方針を整理する
\(y=\frac{\log x}{x}\)のグラフは頻出なので概形は覚えておいて損はないです。改めて解答の方針を整理しましょう。
\(f(x)=\frac{\log x}{x}\)とおいて, \(x>0\)の範囲の増減を調べてみます。
\(f'(x)=\frac{1-\log x}{x^2}\)となるから, 増減表は下のようになります。
![]()
\(f(x)\)は\(x>0\)の範囲で最大値\(f(e)=\frac{1}{e}\)と取るから,求める範囲は\(\frac{1}{e}\leqq a\)となります。
おわりに
![]()
今回は「不等式の成立条件」についてお話ししました。
数学Ⅰ, Ⅱ, Ⅲでは様々な関数について学習します。そのとき, グラフの概形と最大値や最小値について学びますが, その応用先として方程式や不等式に関する問題があります。グラフを利用して方程式や不等式に関する問題を解くことは高校数学の1つのテーマですので是非理解してほしいところです。
また, 1つの考え方で様々な問題が解けるようになります。解法暗記ではなく, その解法の理解を心掛けてください。
それでは,今回はこの辺で!





![[コラム]深呼吸のしかた](https://sp-ao.shortpixel.ai/client/to_auto,q_glossy,ret_img,w_150,h_150/https://www.educational-lounge.com/wp-content/uploads/2018/12/SHI0322006_TP_V4-150x150.jpg)

![[AO・推薦]評定平均値を意識しておこう](https://sp-ao.shortpixel.ai/client/to_auto,q_glossy,ret_img,w_150,h_150/https://www.educational-lounge.com/wp-content/uploads/2019/05/0fb723cb709312930f2aaf32fb389602_s-150x150.jpg)

![[地学基礎]11月の学習指針②(高1・高2)](https://sp-ao.shortpixel.ai/client/to_auto,q_glossy,ret_img,w_150,h_150/https://www.educational-lounge.com/wp-content/uploads/2019/01/tokunoshimaIMGL4658_TP_V-150x150.jpg)
![[政治経済]12月から意識すべきこと(高1・2)①](https://sp-ao.shortpixel.ai/client/to_auto,q_glossy,ret_img,w_150,h_150/https://www.educational-lounge.com/wp-content/uploads/2018/12/PAK75_kokkaimaenodouro20140905154343_TP_V-150x150.jpg)

